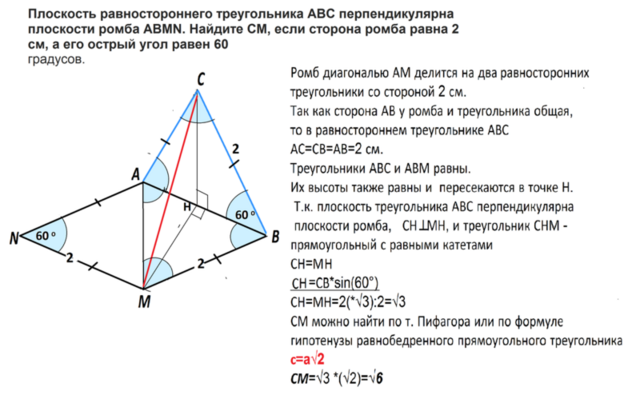
Ромб диагональю АМ делится на два равносторонних треугольника со стороной 2 см.
Так как сторона АВ у ромба и треугольника общая, то в равностороннем треугольнике АВС стороны равны АС=СВ=АВ=2 см.
Треугольники АВС и АВМ равны.
Их высоты также равны и пересекаются в точке Н.
Т.к. плоскость треугольника АВС перпендикулярна плоскости ромба, СН⊥МН, и треугольник СНМ - прямоугольный с равными катетами СН=МН
СН=СВ*sin(60°)
СН=МН=2(*√3):2=√3
СМ можно найти по т. Пифагора или по формуле гипотенузы равнобедренного прямоугольного треугольника
с=a√2
СМ=√3 *(√2)=√6