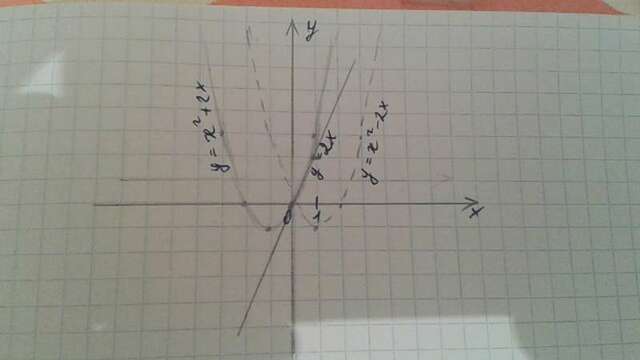
1)Находишь точки касания, функцию приравниваешь к 0, получаешь два уравнения, т.к. там модуль, решаешь их сведением к совокупности:
х^2+2х=4х
-х^2-2х=4х
Отсюда: х1=2; х2=0 =>(2;0),(0;0) - координаты точек касания
2)Составляешь уравнение касательной: в точке(0;0) f(0)=0; находишь производную функции f'(x)=2x+2-4x/|x|, f'(0)=2, отсюда уравнение касательной по формуле у=f(x0)+f'(x0)(x-x0) будет у=2х
3)Строишь графики(на фотке)