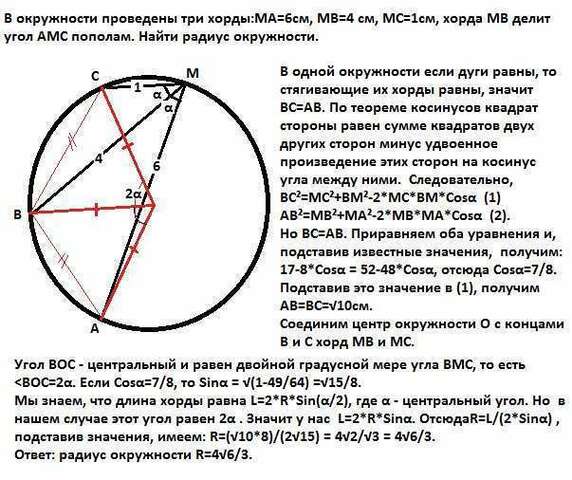
В одной окружности если дуги равны, то стягивающие их хорды равны, значит ВС=АВ.
По теореме косинусов квадрат стороны равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними. Следовательно,
ВС²=МС²+ВМ²-2*МС*ВМ*Cosα (1)
АВ²=МВ²+МА²-2*МВ*МА*Cosα (2).
Но ВС=АВ. Приравняем оба уравнения и, подставив известные значения, получим:
17-8*Cosα = 52-48*Cosα, отсюда Cosα=7/8.
Подставив это значение в (1), получим АВ=ВС=√10см.
Соединим центр окружности О с концами В и С хорд МВ и МС.
Угол ВОС - центральный и равен двойной градусной мере угла ВМС, то есть Если Cosα=7/8, то Sinα = √(1-49/64) =√15/8.
Мы знаем, что длина хорды равна L=2*R*Sin(α/2), где α - центральный угол. Но в нашем случае этот угол равен 2α . Значит у нас L=2*R*Sinα. ОтсюдаR=L/(2*Sinα) , подставив значения, имеем: R=(√10*8)/(2√15) = 4√2/√3 = 4√6/3.
Ответ: радиус окружности R=4√6/3.