Равнобокая трапеция описана около окружности с радиусом 12 дм , точка касания делит ее...

Question

Равнобокая трапеция описана около окружности с радиусом 12 дм , точка касания делит ее боковую сторону в соотношении 9:4. Найдите среднюю линию трапеции

Answer 1

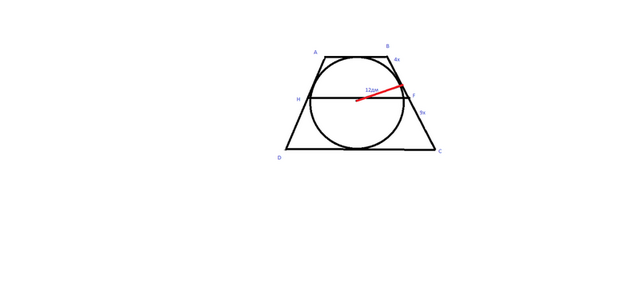
по свойству вписанной окр в трапецию т,е  т,е  опять же: x==4, а значит вся сторона = 8+18 = 26 
Окр можно вписать в трапецию тогда и только тогда, когда сумма сторон
( боковых ) = сумме оснований т,е 26+26=52 ( AD+BC ) и это равно сумме оснований т,е 52 = AB+DC, 52=52
Средняя линия = полусумме оснований т,е  = 26
( ср линия ) 

---