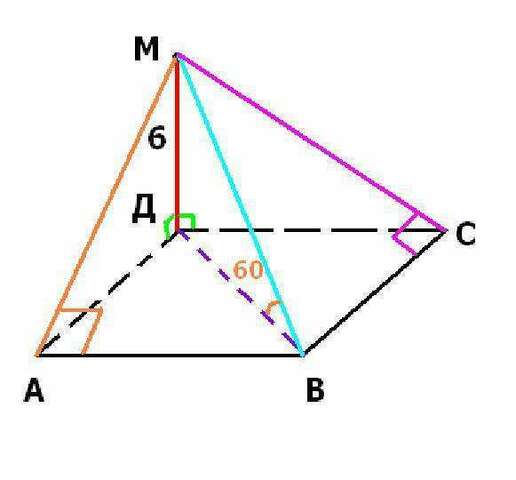
АВСД - квадрат, МД перпенд (АВД), МД = 6 см, уг МВД = 60
Б)
Т.к. МД перпенд (АВД), то МД перпенд ДВ, тогда уг МДВ = 90 град.
Из треуг МДВ:
уг МДВ = 90, уг МВД = 60, тогда уг ДМВ = 180 - (90 + 60) = 30 град, тогда
МВ = 2*ДВ, поскольку ДВ лежит напротив угла в 30 град.
Тогда по т Пиф:
(2ДВ)^2 = МД^2 + ДВ^24
ДВ^2 = 36 + ДВ^2
3ДВ^2 = 3
6ДВ^2 = 12
ДВ = 2V3 см, также МВ = 2*ДВ = 4V3 см.
Из треуг АДВ: уг ДАВ = 90, АД = АВ (усл),
тогда по т Пиф АД = V6 см.
А)
Т.к. МД перпенд (АВД), то уг МДС = 90. Т.к. АВСД квадрат, то АД || CB, тогда МД и СВ - скрещивающиеся и поскольку МД перпенд АД, то уг МСВ = 90 град, тогда треуг МСВ прямоугольный. Треуг МАВ рассматривается аналогично.
В)
Чтобы получить проекцию треуг МАВ на (АВС) нужно опустить перепендикуляры из всех вершин треуг МАВ на (АВС), но точки А, В и так принадлежат пл-ти (АВС). Поэтому, т.к. т.А и т.В прин (АВС) и МД перпенд (АВС), то треуг ДАВ является проекцией треугольника МАВ на плоскость (АВС).
Из треуг АДВ:
уг ДАВ = 90, АД = АВ (усл), тогда по т Пиф
АД = V6 см, тогда
Sдав = 1/2 * V6 * V6 = 3 см квадратных.
P.S. V - это знак квадратного корня.