В параллелограмме ABCD угол А=60°, диагональ BD перпендикулярна к стороне АВ. Прямая,...

Question

В параллелограмме ABCD угол А=60°, диагональ BD перпендикулярна к стороне АВ. Прямая, проходящая черкз середину отрезка - точку М - параллельно АD, пересекает сторону AB в точке К, МК=4см
- Найдите S параллелограмма ABCD
- Найдите S треугольника AMD.

Answer 1

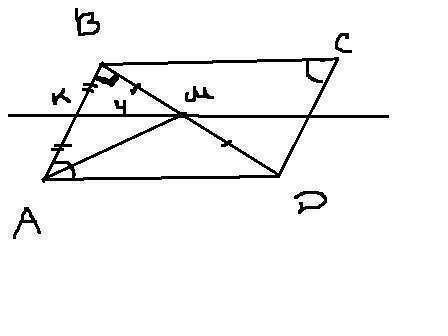
А) 1) ВМ=МD (т.к. т. М - середина ВD) ⇒ т.К - середина АВ, т.е. ВК=АК
⇒ КМ - средняя линия треугольника АВD 
КМ=1/2АD ⇒ АD=4*2=8 см
2) т.к. DВ перпендикулярна АВ, то угол DВА=90 ⇒ угол ВDА=180-(90+60)=30
3) сторона лежащая против угла в 30 градусов = 1/2 гипотенузы 
⇒ АВ=1/2АD = 4
4) Sabcd = AD*AB*sin60=8*4*√3/2=16√3
б) 1) найдем ВD по т.Пифагора = √8²-4²=√48=4√3
т.к. КМ - средняя линия, то ВМ=MD=4√3/2=2√3
2) сумма всех углов в параллелограмме = 360
⇒ угол D= углу В = 360-(уголА+уголС)/2=360-120/2=120
накрест лежащие углы равны, значит угол МDА=120/2=60
3) Samd=2√3*8*sin60/2=2√3*4*√3/2=4√3*8*√3/2=4*√3*4*√3=16*3=48

---