В прямоугольном треугольнике ABC с прямым углом С проведена медиана СМ. Найдите AB, если CM = 1 см
В прямоугольном треугольнике медиана, проведенная из прямого угла к гипотенузе, равна ее половине.
Следовательно, СМ=АВ:2, АВ=2*СМ=2 см
--------
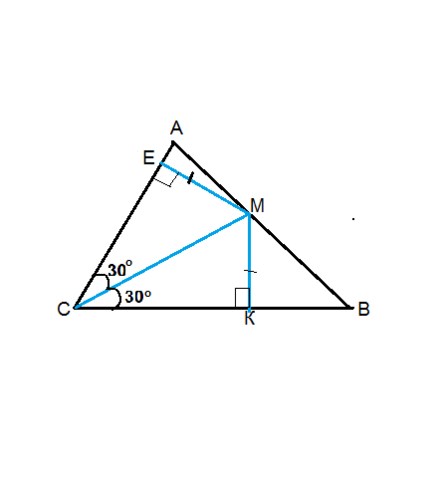
В треугольнике АВС с углом С, равным 60°, проведена биссектриса СМ. Найдите расстояние от точки М до сторон АС и ВС, если СМ=20 см
Расстояние от любой точки биссектрисы угла до его сторон одинаково для данной точки биссектрисы.
На данном во вложении рисунке угол С=60°, биссектриса СМ делит его на два равных угла по 30°
Расстояние от точки до прямой измеряют перпендикуляром.
МЕ ⊥ АС, МК ⊥ ВС
⊿ СЕМ=⊿ СКМ по равному острому углу и общей гипотенузе.
ЕМ=МК.
Катет, противолежащий углу =30° равен половине гипотенузы.
ЕМ=МК=20:2=10 см
-----
Дан прямоугольный треугольник АВС с прямым углом С.
Найдите ∠А, если:
а)∠В=4∠А,
б)3∠В-5∠А=6°
Сумма острых углов прямоугольного треугольника равна 90°⇒
а)
∠В+∠А=90
°
∠В=4∠А, ⇒
4∠А+∠А=90°
5∠А=90°
∠А=90:5=
18°
б)
3∠В-5∠А=6°
∠В+∠А=90°
∠В=90°-∠А
3(90°-∠А)-5∠А=6°
270°-3 ∠А-5∠А=6°
264°=8∠А
∠А=33°