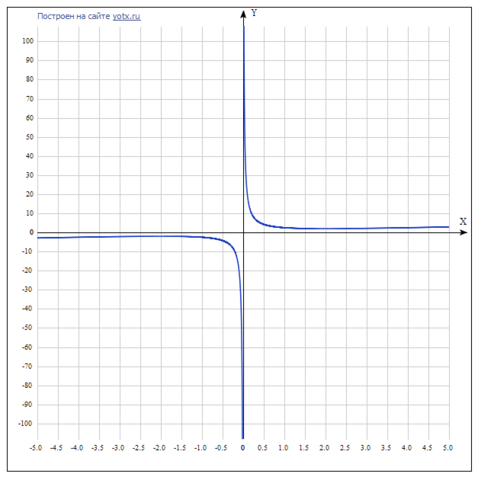
F(x) = x/2 + 2 / x
Область определения функции Точки, в которых функция точно не определена:x1 = 0 Точки пересечения с осью координат XГрафик функции пересекает ось X при f = 0 значит надо решить уравнение:x /2 + x / 2 = 0 Решения не найдено,значит, график не пересекает ось X Точки пересечения с осью координат Y График пересекает ось Y, когда x равняется 0:подставляем x = 0 в x/2 + 2/x.f(0) = zoo значит f(x) не пересекает Y
Экстремумы функции Для того, чтобы найти экстремумы,нужно решить уравнениеd
--(f(x)) = 0
dx (производная равна нулю),и корни этого уравнения будут экстремумами данной функции:d
--(f(x)) =
dx 1 2
- - -- = 0
2 2
x Решаем это уравнение Корни этого ур-нияx 1 = -2x2 = 2Зн. экстремумы в точках:(-2, -2)(2, 2).
Интервалы возрастания и убывания функции:Найдём интервалы, где функция возрастает и убывает, а также минимумы и максимумы функции, для этого смотрим как ведёт себя функция в экстремумах при малейшем отклонении от экстремума:Минимумы функции в точках:x2 = 2 Максимумы функции в точках:x2 = -2Убывает на промежутках(-oo, -2] U [2, oo)Возрастает на промежутках[-2, 2]Точки перегибов Найдем точки перегибов, для этого надо решить уравнение 2
d
---(f(x)) = 0
2
dx (вторая производная равняется нулю),корни полученного уравнения будут точками перегибов для указанного графика функции, 2
d
---(f(x)) =
2
dx 4
-- = 0
3
x Решаем это уравнение Решения не найдены, значит перегибов у функции нет. Вертикальные асимптоты Есть:x1 = 0 Горизонтальные асимптоты Горизонтальные асимптоты найдём с помощью пределов данной функции при x->+oo и x->-oo x 2
lim - + - = -oo
x->-oo2 x значит,горизонтальной асимптоты слева не существует x 2
lim - + - = oo
x->oo2 x значит,горизонтальной асимптоты справа не существует Наклонные асимптоты Наклонную асимптоту можно найти, подсчитав предел функции x/2 + 2/x, делённой на x при x->+oo и x->-oo x 2
- + -
2 x
lim ----- = 1/2
x->-oo x значит,уравнение наклонной асимптоты слева: y = х /
2 x 2
- + -
2 x
lim ----- = 1/2
x->oo x значит,уравнение наклонной асимптоты справа: y = х / 2
Чётность и нечётность функции Проверим функция чётна или нечётна с помощью соотношений f = f(-x) и f = -f(-x).Итак, проверяем:x 2 2 x
-- + -- = - -- - -
1 1 1 2
2 x x - Нетx 2 -2 -x
-- + -- = - --- - ---
1 1 1 2
2 x x - Нет значит, функция не является ни чётной ни нечётной