Рисунки к задачам не подписала, нетрудно понять, к какой задаче они относятся.
--------------------------------------------------------------------------------
2) Без рисунка
Площадь осевого сечения цилиндра 12√π дм² а площадь основания равна 64 дм² Найдите высоту цилиндра.
Площадь осевого сечения - произведение высоты цилиндра на диаметр его основания.
Высоту цилиндра найдем из формулы:
S сечения цилиндра=DH, где D- диаметр основания цилиндра.
D=2r
Socнов=πr²=64
r²=64:π
r= 8:√π
D= 16:√π
Н = Sсечения : D
H=12√π: (16:√π)=12π:16=3π/4 дм
Проверка:
S=DH= (16:√π)*3π/4=12√π дм²
----------------------------------------------------------------------------------------
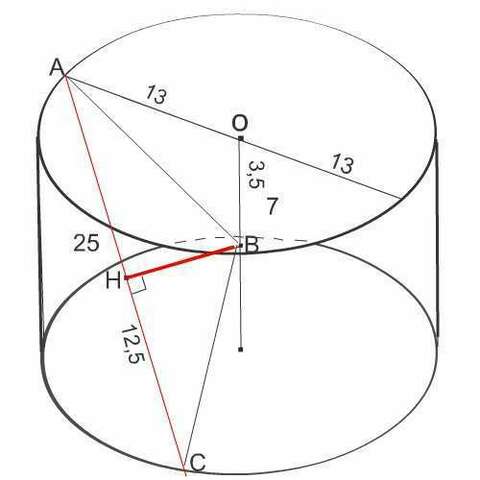
3)Отрезок СД равен 25 см, его концы лежат на разных окружностях основания цилиндра.
Найдите расстояние от отрезка СД до основания цилиндра, если его высота 7 см,
а диаметр основания 26.
(???)-не поняла.
(СД пересекается с обоими основаниями. От какого места отрезка нужно найти расстояние?Может, не до основания, а до оси цилиндра? В таком случае задача имеет смысл)
---------------------------------------------------------------------------
6) Рисунок.
Отрезок ДЕ-хорда основания конуса, которая удалена от оси конуса на 9 см.
Отрезок КО-высота конуса, причем КО=3√3 см .
Найдите расстояние от точки конуса О (центр основания конуса) до плоскости, проходящей через точки Д , Е и К.
ОР- высота прямоугольного треугольника КОМ с катетами КО= 3 √3 и ОМ=9
КМ=√(ОМ² +КО² )=√(81+27)=√108=6√3
Сравним гипотенузу КМ и катет КО в прямоугольном треугольнике КОМ
КО=КМ:2
Следовательно, угол КМО=30 градусов.
ОР- противолежит углу 30 градусов в прямоугольном треугольнике ОРМ и равен половине гипотенузы ОМ
ОР=9:2=4,5 см
---------------------------------------------------------------------------
7) Рисунок.
Сфера w проходит через вершины квадрата CDEF, сторона которого равна 18 см.
Найдите расстояние от центра сферы -точки О - до плоскости квадрата, если радиус ОЕ сферы образует с плоскостью квадрата угол, равный 30 градусам.
Рассмотрим рисунок.
Искомое расстояние ОН - катет треугольника ЕНО, противолежащий углу 30°.
Центр Н квадрата СDEF- точка пересечения его диагоналей.
ЕН- половина диагонали квадрата.
Диагональ найдем по формуле диагонали квадрата:
D=а√2=18√2
ЕН=18√2:2=9√2
ОН:ЕН=tg (30°)=1/√3
ОН=ЕН·1/√3
ОН=9√2·1/√3
Умножим числитель и знаменатель дроби 9√2:√3 на√3. Её величина от этого не изменится, зато может принять более удобный вид.
9√2·√3:√3·√3=9√6·3=3√6 см
ОН=3√6 см
----------------------------------------
8) Рисунок.
Стороны треугольника МNK касаются шара.
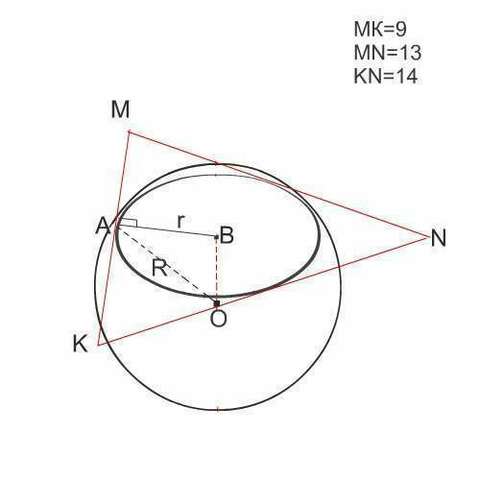
Найдите радиус шара, если МК=9,МN=13,KN=14 и расстояние от центра шара О до плоскости MNK равно √6
Поскольку все стороны треугольника касаются шара, сечение шара этим треугольником - круг, а окружность, которая его ограничивает - вписанная в треугольник.
Рассмотрим рисунок.
Радиус шара R найдем из прямоугольного треугольника АВО, катетами в котором являются радиус АВ=r сечения шара треугольником МNK,
и расстояние ОВ от центра шара до плоскости треугольника МNK, а гипотенузой - АО= радиусу R шара.
Радиус сечения вычислим по формуле радиуса вписанной в треугольник окружности:
r=√{(p−a)(p−b)(p−c):p}
где а, в, с - стороны треугольника, р - его полупериметр
r=√{4*5*9:18=√10
R=√(АВ²+ВО²)=√(10+6)=4
Ответ:радиус шара равен 4