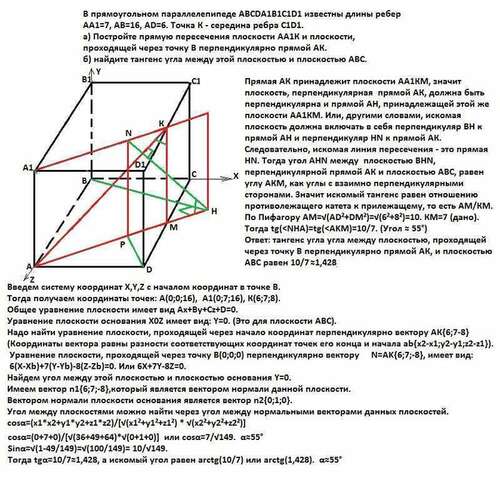
В прямоугольном параллелепипеде АВСDA1B1C1D1 известны длины ребер: АА1=7, АВ=16, AD=6. Точка К - середина ребра С1D1.
а) Постройте прямую пересечения плоскости АА1К с плоскостью, проходящей через
точку В перпендикулярно прямой АК.
б) Найдите тангенс угла между этой плоскостью и плоскостью АВС. ________________________________________________________________
Цитата: "Прямоугольный параллелепипед — объёмная фигура, у которой шесть граней, и каждая из них является прямоугольником."
а) Если прямая перпендикулярна плоскости , то она перпендикулярна любой прямой в этой плоскости.
Прямая АК принадлежит плоскости АА1КМ, значит плоскость, перпендикулярная прямой АК, должна быть перпендикулярна и прямой АН, принадлежащей этой же плоскости АА1КМ. Или, другими словами, искомая плоскость должна включать в себя перпендикуляр ВН к прямой АН и перпендикуляр НN к прямой АК. Следовательно, искомая линия пересечения - это прямая НN. Тогда угол АНN между плоскостью ВНN,
перпендикулярной прямой АК и плоскостью АВС, равен углу АКМ, как углы с взаимно перпендикулярными сторонами. Значит искомый тангенс равен отношению противолежащего катета к прилежащему, то есть АМ/КМ.
По Пифагору АМ=√(AD²+DM²)=√(6²+8²)=10. КМ=7 (дано).
Тогда tg(Ответ: тангенс угла угла между плоскостью, проходящей через точку В
перпендикулярно прямой АК, и плоскостью АВС равен 10/7≈1,428.
Решение координатным методом.
Введем систему координат X,Y,Z с началом координат в точке В.
Тогда получаем координаты точек: А(0;0;16), А1(0;7;16), К(6;7;8).
Общее уравнение плоскости имеет вид Ax+By+Cz+D=0.
Уравнение плоскости основания Х0Z имеет вид: Y=0. (Это для плоскости АВС).
Надо найти уравнение плоскости, проходящей через начало координат перпендикулярно вектору АК{6;7-8} (Координаты вектора равны разности соответствующих координат точек его конца и начала:
ab{х2-х1;y2-y1;z2-z1}).
Уравнение плоскости, проходящей через точку В(0;0;0) перпендикулярно вектору N=AK{6;7;-8}, имеет вид 6(X-Xb)+7(Y-Yb)-8(Z-Zb)=0. Или 6Х+7Y-8Z=0.
Найдем угол между этой плоскостью и плоскостью основания Y=0.
Имеем вектор n1{6;7;-8},который является вектором нормали данной плоскости. Вектором нормали плоскости основания является вектор n2{0;1;0}.
Угол между плоскостями можно найти через угол между нормальными векторами данных плоскостей.
cosα=(x1*x2+y1*y2+z1*z2)/[√(x1²+y1²+z1²) * √(x2²+y2²+z2²)]
cosα=(0+7+0)/[√(36+49+64)*√(0+1+0)] или cosα=7/√149. α≈55°
Sinα=√(1-49/149)=√(100/149)= 10/√149.
Тогда tgα=10/7≈1,428, а искомый угол равен arctg(10/7) или arctg(1,428). (α≈55°).