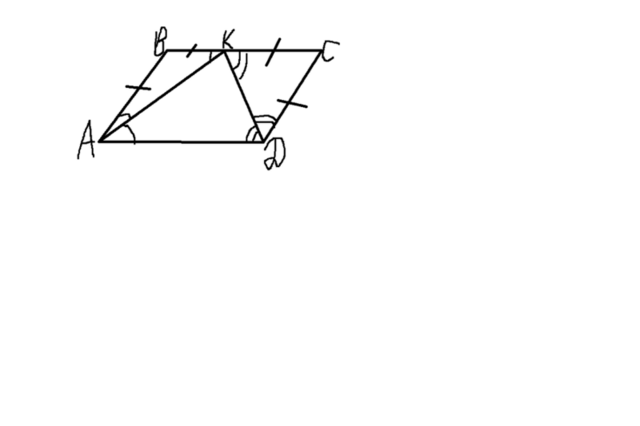
Пусть биссектрисы пересеклись в точке K. (см. вложение) Тогда угол BAK равен углу KAD, так как AK-биссектриса; угол KAD равен углу BKA как внутренние накрест лежащие при параллельных прямых BC и AD и секущей AK. Значит, углы BAK и BKA - равны, следовательно, треугольник ABK - равнобедренный (по признаку), и BA=BK. Аналогично доказывается, что KC=CD. Но AB=CD, т.к. ABCD-параллелограмм. Значит, BC=BK+KC=AB+CD=AB+AB=2*AB. То есть,