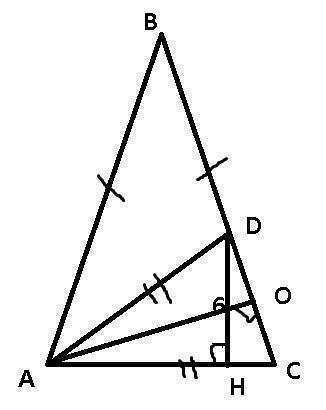
Т.к треугольник АВС- равнобедренный, то углы при основании равны(угол А= углу= С). АD биссектриса=> делит угол А пополам. Тогда угол С в 2 раза больше больше угла DAC. Пусть угол DAC=x; тогда угол С=2x.
Биссектриса угла при основании равнобедренного треугольник равна основанию. Тогда треугольник ADC- равнобедренный. Углы при основании равны(угол С = углу ADC= 2x) . Отсюда выражаем сумму углов, равную 180.
2x+2x+x=180
5x=180
x=36
тогда угол DAC=36, ADC=C= 72.
DH- расстояние, т.е не что иное, как высота. угол DHA=90, DAH=36
sin(DAH)= DH/AD; AD=AC=6/sin36.
DC∈BC. А т.к треугольник АDC- равнобедренный, то (расстояние)высота АО будет являться и биссектрисой и медианной.
=> угол ОАС= 18, cosOAC=AO/AC.
cos18=AO/(6/sin36)
AO= (6cos18)/sin36