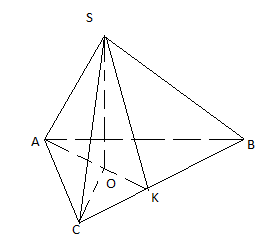
В основе лежить правильный треугольник

кв. ед.
Sбок = 1/2 Po * SK
OK - радиус вписанной окружности треугольника ABC

- OK
OC - радиус описанной окружности

С прямоугольного треугольника SOC (SOC = 90 градусов)

С прямоугольного треугольника SOK (

Sбок =

Sбок : So =

P.S. нужно проверить всё))