Функция убывает и возрастает на промежутках, где производная этой функции отрицательна или положительна соответственно.
1) Найдем производную и нули функции:
y=cosx + 2x;
y'= 2 - sinx;
2 - sinx = 0;
sinx = 2 - решений нет, так как функция sinx существует на промежутке [-1;1]
2) Найдем производную и нули функции:
y=x + 1/x ;
;
y'=1 - 1/x^2 = (x^2 - 1)/x^2.
(x^2 - 1)/x^2 = 0; ОДЗ: x≠0
x^2 - 1 = 0;
x = -1 или x = 1
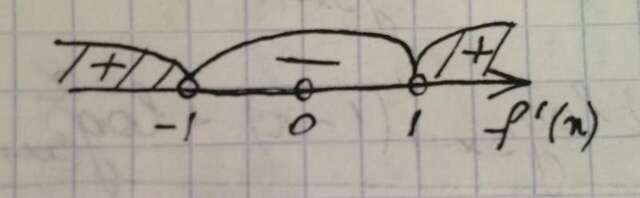
Определим промежутки с помощью метода интервалов (на фото)...
Так как производная положительна на промежутках (-∞;-1) и (1;+∞), то функция (1) возрастает на этих промежутках.
Ответ: (-∞;-1)∪(1;+∞)