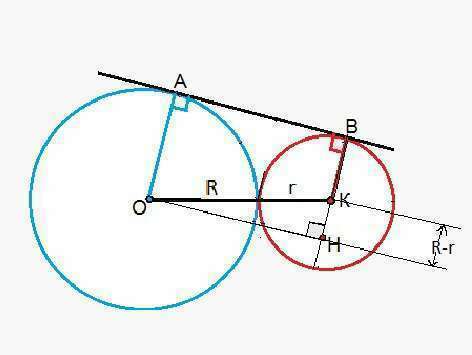
Пусть окружности с центром О и радиусом R касается внешним образом с окружностью с центром К и радиусом r.
АВ - отрезок общей касательной.
Углы ОАВ=КВА=90°, как радиусы, проведенные к касательной в точку касания.
Соединим центры окружностей отрезком ОК.
Из центра О большей окружности проведем параллельно АВ прямую до пересечения с диаметром меньшей окружности в точке Н.
Четырехугольник АОНВ - прямоугольник.
ОН=АВ
Треугольник ОНК - прямоугольный.
ОК- в нем гипотенуза, ОН и ОК- катеты.
По т. Пифагора
ОН²=ОК²-КН²
ОК=R+r
KH=R-r
OH²=(R+r)²-(R-r)²
OH²=R²+2Rr+r² -R²+2Rr-r²
OH²=2Rr+2Rr
OH²=4Rr=2R*2r=D*d, что и требовалось доказать.