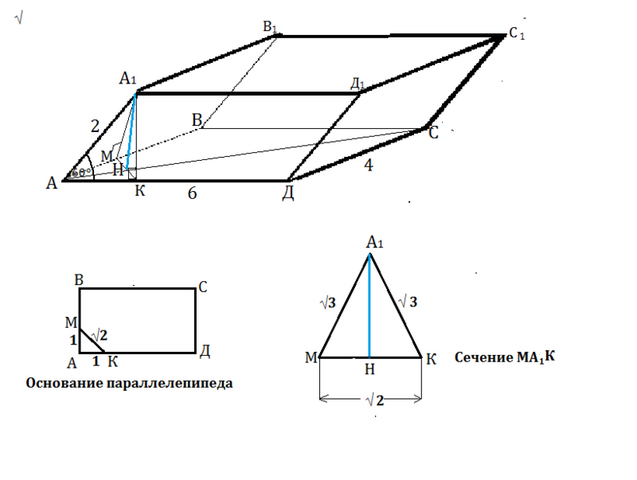
Основанием наклонного параллелепипеда является прямоугольник со сторонами 4 см и 6 см. Боковое ребро равно 2 см и образует со смежными сторонами основания углы в 60°. Найти объем параллелепипеда.
Подробное решение.
Объем параллелепипеда равен произведению его высоты на площадь основания.
V=S*h
Т.к. основание - прямоугольник, площадь его равна произведению сторон.
S=4*6=24 см²
Высоту параллелепипеда нужно найти.
Сделаем рисунок параллелепипеда.
Ребро АА₁ образует со смежными сторонами основания углы А₁АМ и А1АК в 60°.
А₁МК - равнобедренный треугольник, т.к. А₁М и А₁К - катеты равных прямоугольных треугольников с равными острыми углами и общей гипотенузой АА₁.
А₁
К=АА₁*sin (60º)=(2√3)/2=
√3 см
Сумма острых углов прямоугольного треугольника равна 90º, следовательно, угол АА1К=90º -60º=
30ª
АК=АМ=2*sin(30º)=2*0,5=
1 см
Высота параллелепипеда - перпендикуляр
А₁Н, опущенный из А₁ на основание. В то же время А₁Н - высота равнобедренного треугольника МА₁К.
Так как основание параллелепипеда - прямоугольник, МК - гипотенуза равнобедренного прямоугольного треугольника и по свойству гипотенузы такого треугольника
МК=АК*√2=1*√2=√2.
В треугольнике МА1К половина основания НК=МК:2=(√2):2
По т.Пифагора
НА₁²=А₁
К² - НК²
А₁
Н=√(3-2/4)=√2,5=5/√10=0,5√10 см
V=S( АВСД)*h=24*0,5√10=12√10
см³