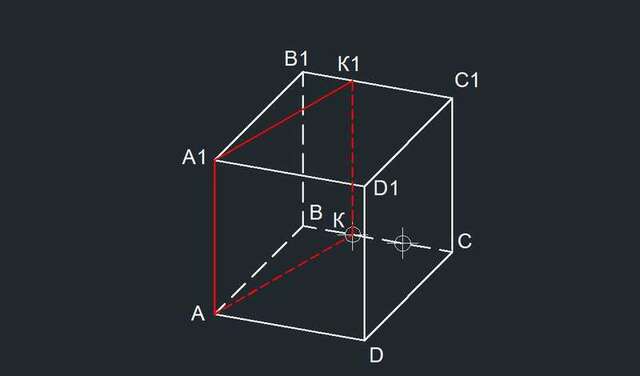
1) Сначала находим точку К, поделив ВС на 3 части.
Проводим АК, затем КК₁ параллельно АА₁ и на верхней грани А₁К₁.
2) Ребро АА₁ перпендикулярно плоскости АВСД и, следовательно перпендикулярно отрезку АК, который лежит в .этой плоскости.
Отрезок КК₁ лежит в плоскости ВВ₁С₁С, перпендикулярной основе параллелепипеда. То есть все углы прямые.
3) Для определения площади сечения АА₁К₁К, если ав=а, аа1=3а находим АК =√(а²+(а/3)²) = √((9а²+а²)/9) = (а/3)√10.
Тогда S = 3a*(а/3)√10 = a²√10.