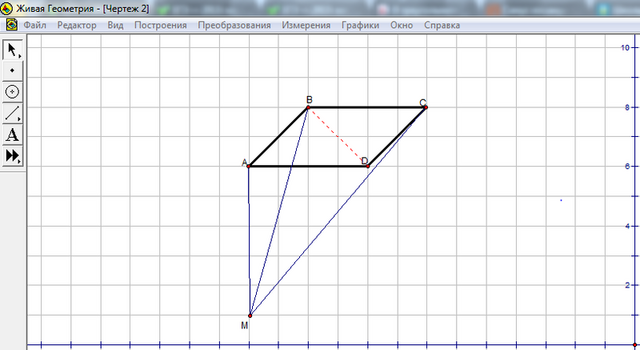
Я сделала чертеж, чтоб было понятнее.
Дано: АВСD- параллелограмм,
АВ лежит в плоскости АВМ,
угол между ВС и пл.АВМ = φ,
а) АВСD — квадрат;
б) АВСD — ромб, в котором B = 120°
Найти: угол между диагональю ВD и пл.АВМ-?
Решение: !С самого начала стоит сказать, что угол между ВС и пл.АВМ - это уголABC(или угол B), т.е. это уголφ
а)1)Т.к. АВСD — квадрат, то все углы = по 90°., т.е. угол B=90°.
2)В квадрате диагональ является биссектрисой угла, т.е диагональ BD делит угол B пополам, т.е. уголABD(а это угол между диагональю ВD и пл.АВМ)=45 °.
Ответ:45 °
б)Т.к. АВСD — ромб, в котором B = 120°, а в ромбе диагонали делят его углы пополам, т.е. диагональ BD, выходящая из угла B, делит го пополам, т.е. уголABD(а это угол между диагональю ВD и пл.АВМ)=60°
Ответ:60°