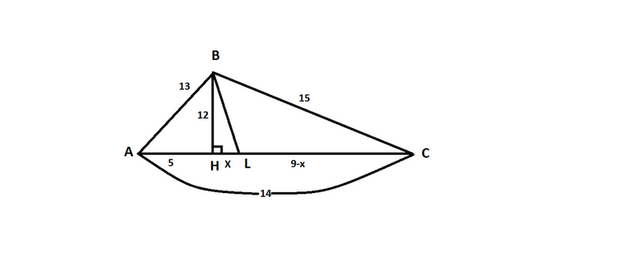
По формуле Герона найдем площадь треугольника:S= √(р(р-а)(р-в)(р-с)),
где а=13, в=14, с=15, р=(а+в+с)/2=(13+14+15)/2=21 ⇒
S=√(21(21-13)(21-14)(21-15))=√(21*8*7*6)=√7056=84
S=84.
ВН-высота, S=вh/2 ⇒ h=2S/в=2*84/14=12; ВН=12.
АН=√(АВ²-ВН²)=√(169-144)=√25=5; АН=5.
НС=АС-АН=14-5=9; НС=9.
по свойству биссектрисы: АL/LС=АВ/ВС
пусть НL=x, тогда AL=5+x, LC=9-x ⇒
АL/LС=АВ/ВС ⇔ (5+x)/(9-x)=13/15
15(5+x)=13(9-x)
75+15x=117-13x
28x=42
x=42/28=1.5
HL=1.5
SΔHBL=BH*HL/2=12*1.5/2=9
отв:9