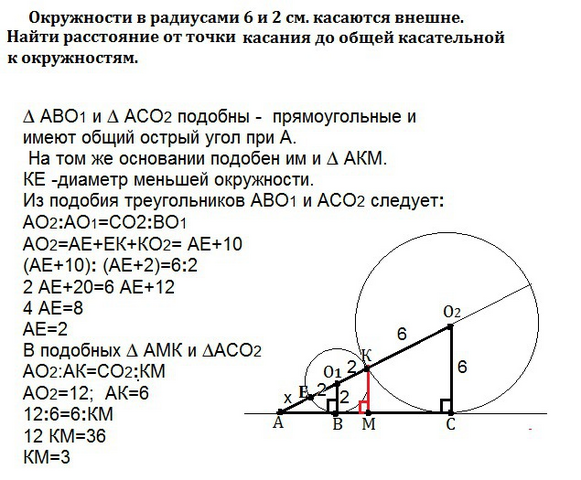
Окружности в радиусами 6 и 2 см. касаются внешне. Найти расстояние от точки касания до общей касательной к окружностям.
-------
Обозначим центр меньшей окружности О₁1, большей - О₂2.
Точку касания окружностей - К, точку пересечения перпендикуляра из К к касательной - М. ( расстояние - перпендикулярный отрезок)
Соединим О₁ и О₁ прямой и продолжим ее до пересечения с общей касательной в точке А.
Соединив центры окружностей с точками касания, получим прямоугольные треугольники ∆ АВО₁ и ∆ АСО₁. Они подобны - имеют общий острый угол при А. На том же основании подобен им и ∆ АКМ.
КЕ -диаметр меньшей окружности.
Из подобия треугольников АВО₁ и АСО₂ следует:
АО₂:АО₁=СО₂:ВО₁
АО₂=АЕ+ЕК+КО₂= АЕ+10
(АЕ+10): (АЕ+2)=6:2
2 АЕ+20=6 АЕ+12
4 АЕ=8
АЕ=2
В подобных ∆ АКМ и ∆АО₂М
АО₂:АК=СО₂:КМ
АО₂=12, АК=6
12:6=6:КМ
12 КМ=36
КМ=3