X^3 + (1/3)x >= - 26/3

Question

Дан 1 ответ

Kulakca_zn · Answer 1 · 2018-04-02T16:43:29+0000

Для начала перенесём всё влево и умножим обе части неравенства на 3:
$3 x^{3} + x + 26 \geq 0$

Собственно говоря: а что теперь? Вспомните аналогичные неравенства с квадратным трёхчленов в левой части. Там мы без проблем раскладывали левую часть на множители и затем применяли метод интервалов. Здесь история вроде бы должны быть аналогичной, но возникает дополнительная трудность: как разложить кубический трёхчлен на множители? На самом деле, это можно сделать по-разному. Один из способов - угадаем корень данного трёхчлена.
Сразу оговорюсь - это способ работает только в тех случаях, когда многочлен имеет какой-нибудь ЦЕЛЫЙ корень. Если же целых корней квадратный трёхчлен не имеет, то всё не так радужно и надо использовать какой-нибудь другой способ.
Здесь мы сразу махнём наудачу и подберём какой-нибудь целый корень. Чтобы упростить поиск, теория нам говорит: все такие кандидаты надо искать среди делителей свободного члена(в нашем случае, среди делителей числа 26). Вариантов не так много. Какие? +-1, +-2, +-13, +-26. Подставляем их по очереди в наш многочлен. Напомню, что в результате должен получиться 0.
Подстановка +-1 не даёт ровным счётом ничего(в итоге получается не 0).
А вот если x = -2, то получаем
$3 (-2)^{3} - 2 + 26 = -24 - 2 + 26 = -26 + 26 = 0$
Да, здесь нам повезло, и один целочисленный корень многочлена мы нашли.

Что дальше?
Смотрим теорию(а именно, следствие теоремы Безу) и нам становится ясно, что раз x = -2 - корень, то многочлен x - (-2) = x+2 является как раз таки одним из множителей левой части, то есть
$(x+2)Q(x) = 3 x^{3} + x + 26$
Как найти Q(X)? Надо произведение разделить на известный множитель. То есть, сам многочлен на x + 2. Деление многочленов почти напоминает деление чисел, поэтому останавливаться не буду на алгоритме деления. Приведу лишь процесс. Как видим, остаток в итоге получился нулевым.
Теперь мы спокойно раскладываем левую часть на множители.
$(x+2)( 3x^{2} - 6x + 13) \geq 0$
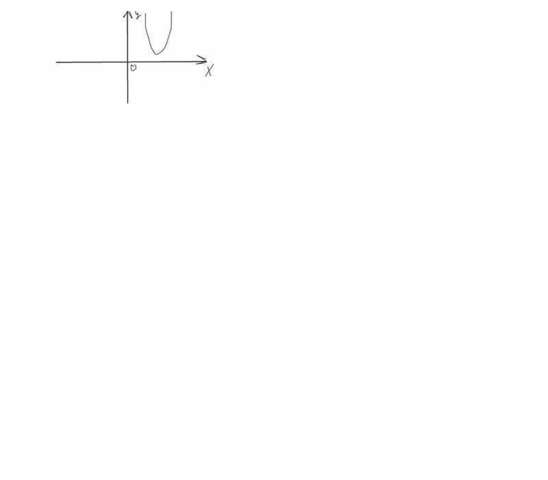
Теперь мы можем разложить на множители квадратный трёхчлен.С этим уже проблем нет. Однако при вычислении дискриминанта получаем, что D = 36 - 12 * 13 < 0, следовательно, корней у данного трёхчлена нет. Значит, нет точек пересечения параболы с осью oX. Более того, ветви параболы соответствующей направлены вверх. Значит, график трёхчлена целиком лежит в верхней полуплоскости. Это показано на рисунке 2. Значит, квадратный трёхчлен не только никогда не сможет обратиться в 0, но и всегда ПОЛОЖИТЕЛЕН. А раз так, то я могу разделить на него обе части неравенства, оставив знак неравенства без изменения(делим на положительное выражение). Поэтому остаётся неравенство
$x + 2 \geq 0$ , откуда
$x \geq -2$
Это и есть ответ.