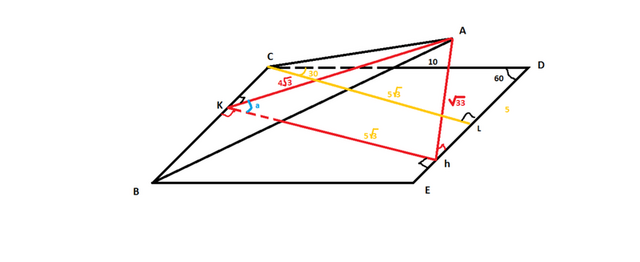
Смотри рисунок.
угол СВЕ=угол СDE=60⁰
CL-высота параллелограмма
ΔСLD-прямоугольный, угол LCD=90°-60°=30° ⇒ LD=0.5*CD=0.5*10=5
CL²=CD²-LD²=10²-5²=100-25=75
CL=√75=5√3
угол между плоскостями измеряется линейным углом АКh=a (угол AKC=угол СКh=90°) из свойства параллелограмма: угол СКh=угол КhE ⇒ Kh-высота ⇒
Kh=СL=5√3
АК-высота ΔАВС, т.к. ΔАВС-равносторонний (сторона=8см),то
СК=0,5*СВ=0,5*8=4
АК²=АС²-СК²=8²-4²=64-16=48
АК=√48=4√3
АК=4√3, Kh=5√3, Ah=√33
для нахождения косинуса угла а воспользуемся теоремой косинусов:
с²=а²+в²-2ав*сosa
cosa=(a²+в²-с²)/2ав=(АК²+Кh²-Ah²) / 2*AK*Kh=(АК²+Кh²*-Ah²) / 2*AK*Kh=
( (4√3)²+(5√3)²-(√33)² ) / 2*4√3*5√3=(48+75-33) / 120=90/120=3/4
отв: cos a=3/4