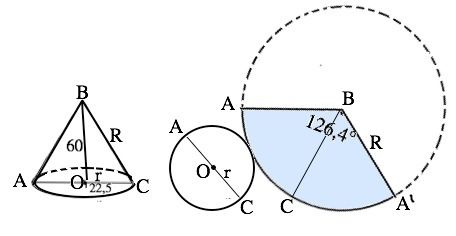
Обозначим конус АВС, АВ=ВС - образующие, О - центр основания, ВО - высота конуса.
Развертка полной поверхности конуса - круг и сектор круга, радиус R которого равен образующей конуса. Построить основание конуса с r=22,5мм -не составит труда.
Длина окружности, ограничивающей основание конуса, l=2πr=45π (мм). Она определяет длину дуги сектора круга радиуса R.
Разберемся с боковой поверхностью.
Из прямоугольного ∆ АВО по т.Пифагора вычислим радиус R сектора, в который развернется боковая поверхность конуса:
R=√(BO²+CO*²)=√4106,25)=64,08 (mm)
Длина окружности с центром В ( центром круга станет вершина конуса) равна: 2π64,08=128,16π (мм)
В полной окружности 360°, на каждый градус приходится:
128,16 π:360°=0,356π (мм)
Тогда боковая поверхность конуса развертывается в сектор круга, длина дуги которого равна длине окружности основания конуса, а угол при В равен:
45π:0,356π=126,4°
В большей окружности проводим радиус, от него с помощью транспортира отложим угол 126,4°. Сектор АВА' - развертка боковой поверхности конуса.
На рисунке в приложении– развертка полной поверхности данного конуса.