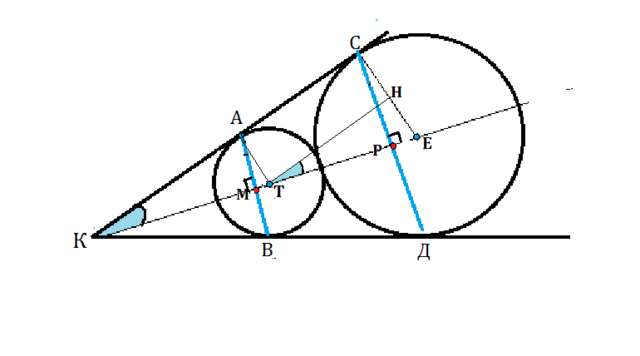
Окружности радиусов 27 и 54 касаются внешним образом. Точки A и B лежат на первой окружности, точки C и D- на второй. При этом AC и BD- общие касательные окружностей. Найдите расстояние между прямыми AB и СD.
--------
Сделаем рисунок.
Обозначим центр меньшей окружности
Т, большей -
Е, точку соединения касательных АС и ВД - К.
Соединим центры окружностей и точки касания с АC.
Углы КАТ=КCЕ=90º
Из Т проведем параллельно АC прямую до пересечения с радиусом CЕ в точке Н.
CН=АТ
НЕ=СЕ- CН=27.
ТЕ=r+R=27+54=81
Косинус угла НЕТ=НЕ:ТЕ=27:81=1/3
Синус угла НЕТ=√(1-cos²∠НЕТ)=
(2√2):3
ТН=ТЕ*sin TEH=81*(2√2):3=
54√2
В треугольнике КCЕ отрезок ТН паралллеьна и =АС - средняя линия.
КC=2 ТН=108√2
КА=АC=54√2
КА=КВ, КС=КД как отрезки касательных из одной точки.
Треугольники КАВ и КСД равнобедренные. КМ и КР - их высоты.
АВ|| СД
Треугольники КАМ и НЕТ подобны - прямоугольные и имеют равный острый угол. ⇒
угол МАК=углу НЕТ и их синусы равны.
КМ=АК*sin∠МАК=(54√2)*(2√2):3=72
АМ || СР
АМ - средняя линия треугольника СКР
МР=КМ=
72 и является расстоянием между АВ и СД