На основании только этих данных доказать подобие трапеций невозможно.
Нарисуем две трапеции по данному в задаче условию.
Сходственные yглы, причем не только два данных, но и все, в трапециях могут быть равны.
Но если основания разныой длины, - а в задаче об этом ничего не сказано,- трапеции подобными не будут. В подобных фигурах пропорциональными должны быть все сходственные стороны и не только стороны.
В подобных многоугольниках пропорциональны все линейные элементы.
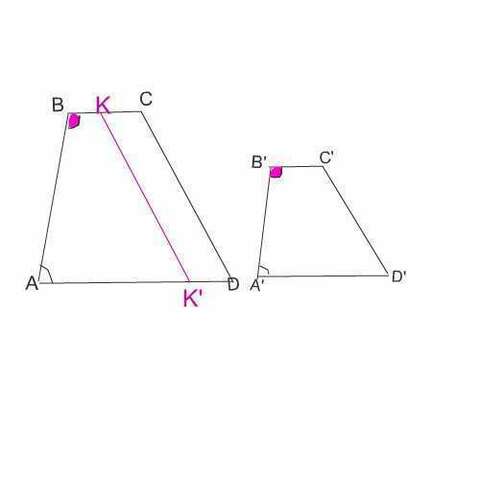
Во вложенном рисунке, где проведена дополнительно сторона KK'=CD, это ясно видно. Хотя по 2 угла равны и боковые стороны трапеций ABKK' и A'B'C'D' пропорциональны, трапеции не подобны, так как основания в них не пропорциональны.
Трапеции ABCD A'B'C'D' подобны, если пропорциональны их основания в дополнение к данным условия задачи.