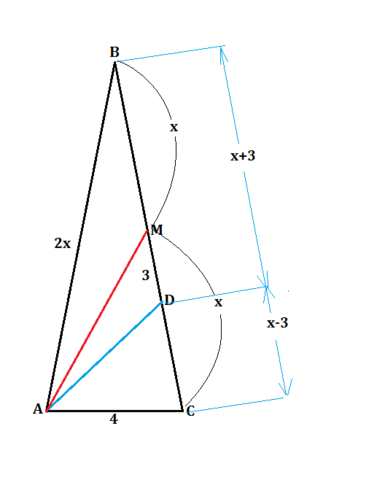
В равнобедренном треугольнике АВС с основанием АС = 4 проведены медиана АМ и биссектриса АD, при этом MD = 3. Найти боковую сторону
------
Сделаем рисунок.
Пусть половина боковой стороны =х
Тогда
АВ=2х,
ВD=
х+3,
СD=
х-3
Биссектриса АD делит ВС в отношении прилежащих сторон. АВ:АС=ВD:DС
2х:4=(х+3):(х-3)
2х*(х-3)=4*(х+3)
После перемножения множителей и приведения подобных членов получим квадратное уравнение
х²-5х-6=0
D=49
х₁=(-(-5)+√49):2=6
x₂=(-(-5)+√49):2=-1 и не подходит.
АВ=ВС=2х=6*2=12