Объем шара находят по формуле:
V=(4/3)*π*R³
Следовательно, для решения задачи нужно найти радиус этого шара. Сделаем рисунок.
Плоскость основания пирамиды лежит на сечении шара.
Сечение - окружность, радиус ОА которой равен 2/3 высоты основания.
Так как радиус ОН вписанной в основание окружности равен 3, а это 1/3 высоты основания, то 2/3 равны 6.
Для нахождения радиуса описанного вокруг пирамиды шара есть формула:
R=b²:2H, где b боковое ребро, Н - высота пирамиды.
Боковое ребро можно найти из прямоугольного треугольника АОМ по т. Пифагора.
АМ²=(ОМ²+ОА²)=52
Тогда
R=b²:2H=52:8=6,5
V=(4/3)*3,14*(6,5)³ =1149,76 ( или, если на полный π умножить в калькуляторе, 1150,346 (ед. объема)
Нужные формулы не всегда во-время вспоминаются.
---------
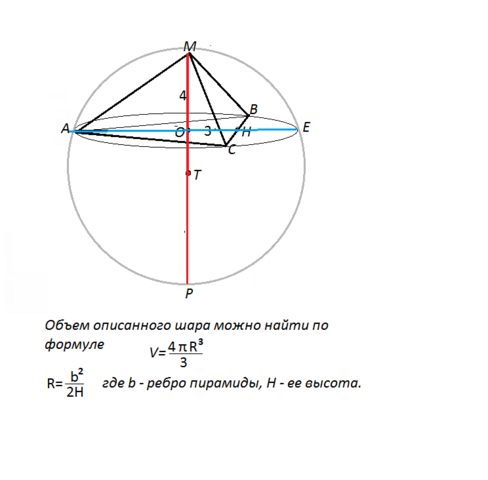
Есть другой способ нахождения этого радиуса. (см. рисунок )
АЕ - диаметр окружности, описанной вокруг основания пирамиды, т.к. основание лежит на этой окружности.
МТ - диаметр шара.
АЕ и МТ - хорды, и произведения их отрезков, образованных точкой пересечения, равны.
Пусть ТР - радиус, отрезок ОТ=х.
АО=ОЕ=6 (см. выше)
Тогда радиус равен МО+ОТ=4+х⇒
МО*ОР=АО*ОЕ
4*(4+х)=6*6
16+4х=36
4х=20
х=2,5⇒
R=4+2,5=6,5
V=(4/3)*3,14*(6,5)³ =1149,76 или более точно 1150,346 (ед. объема)