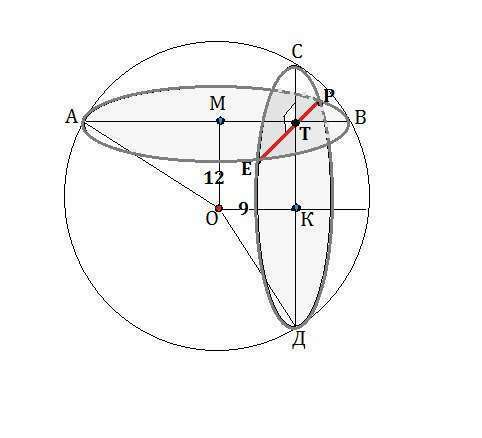
Сделаем рисунок.
Линия пересечения плоскости и сферы - всегда окружность.
Пусть диаметр одной окружности будет АВ, а ее центр - М.
Диаметр второй- СД, а ее центр - К
Центр сферы О удален от первой плоскости на 12 см.
ОМ=12.
ОК=9 см
По т. Пифагора из тр-ка АМО найдем радиус окружности, по которой пересекает сферу первая плоскость:
АМ=√(АО²-МО²)=√(400-144)=16 см
Так же найдем радиус второй окружности:
КД=√(ОД²-ОК²)=√(400-81)=√319 см
Общая хорда сечений - линия ЕР пересечения окружностей.
Хорда пересекает диаметры окружностей в общей точке Т.
Диаметры окружностей перпендикулярны, следовательно, каждый из них перпендикулярен хорде и делит ее пополам.
ЕТ=ТР=х.
Произведения длин отрезков, на которые разбита каждая из пересекающихся хорд, равны:
АТ*ВТ=ЕТ*ТР
МТ=ОК=9 см
ВТ=ВМ-МТ=16-9=7
АТ=АМ+МТ=16+9=25
25*7=х²
х=√175=5√7
ЕР=2*5√7=10√7
Точно так же можно вычислить длину хорды через произведение отрезков диаметра СД второй окружности.
СТ=( √319 -12)
ТД=(√319+12)
СТ*ТД=( √319 -12)*( √319 -12)=319-144=175
Хорда общая, и произведения отрезков диаметров обеих окружностей равны произведению половин хорды.
Длина общей хорды равна 10√7 см