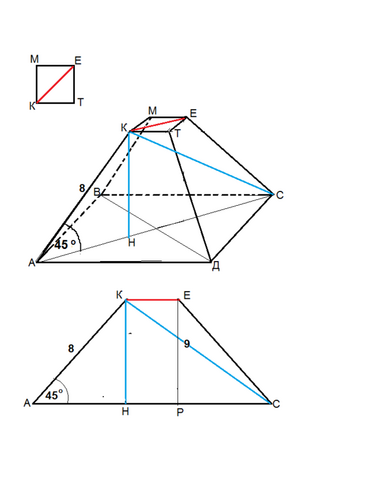
Найдите сторону меньшего основания правильной четырёхугольной усечённой пирамиды, если её боковое ребро равно 8 см и наклонено к плоскости основания под углом 45°, а диагональ пирамиды равна 9 см.
----------
Пирамида правильная, следовательно, основания - квадраты и их плоскости параллельны.
Сделаем и рассмотрим рисунок.
Диагональное сечение пирамиды -
равнобедренная трапеция АКЕС, основаниями которой служат диагонали оснований пирамиды.
Диагональ КС=9 см, боковые стороны равны 8 см.
Углы при большем основании равны 45°
Высота КН перпендикулярна основанию и образует с боковой стороной равнобедренный прямоугольный треугольник АКН.
КН=АН=АК*sin (45°)=4√2 см
Из прямоугольного треугольника КНС по т.Пифагора найдем НС
НС²=КС²-КН²
Т.Пифагора каждый, изучающий стереометрию, знает, поэтому не буду приводить вычисления.
НС=7 см
Из Е опустим перпендикуляр ЕР.
НС=НР+РС
НР=КЕ
РС=АН=47-4√2 см
КЕ=7-4√2 см
КЕ - диагональ меньшего основания.
Его сторона
КТ=КЕ*sin (45°)= [(7-4√2)*√2]:2=(7√2-8):2
КТ=(7√2-8):2 см