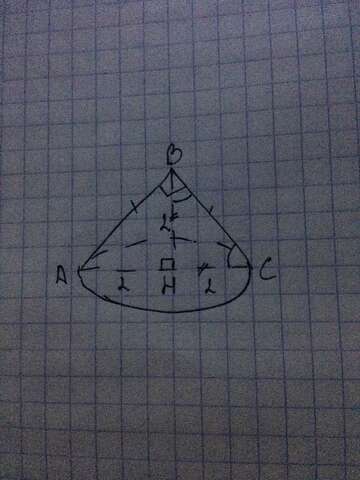
Так как осевое сечение - прямоугольный треугольник, то, угол АВС при вершине конуса - прямой, а треугольник равнобедренный (см. приложение). Проведем высоту ВН к основанию. Так как она проведена к основанию в равнобедренном треугольнике, то она является медианой и биссектрисой. Значит, НС = 2, а угол НВС = BCH = 45. Так как угол ВНС - прямой, то треугольник ВНС - равнобедренный, значит, НС = ВН = 2. А площадь треугольника равна 2*2\2 = 2. Значит площадь всего треугольника АВС = 2+2 = 4. Ответ: 4.