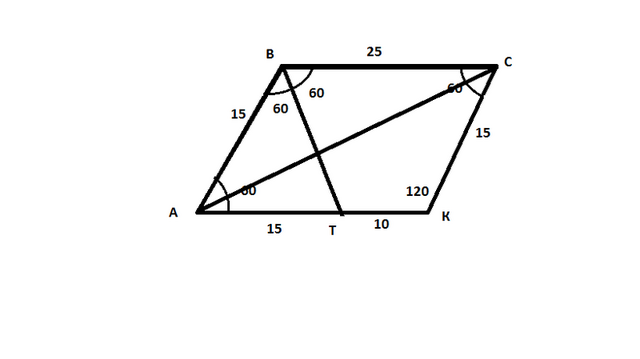
1) Т к ВТ-биссектриса, то угол АВТ=ТВС=60 градусов.В паралелограмме противолежащие стороны параллельны и равны т е ВТ-секущая относительно параллельных прямых ВС и АК => угол СВТ=ВТА=60градусов, тогда треугольник АВТ-равнобокий, а т к два угла по 60 градусов, то третий угол тоже 60 градусов, значит треугольник равносторонний => АВ=АТ=ВТ=15см.
2) т к противолежащие стороны в паралелограмме равны, то ВС=АК=15+10=25см.
Рассмотрим треугольник АВС:
По теореме косинусов: АС² = 15² +25² -2*15*25*cos120 = 225+ 625 + 375 = 1225
АС = √1225 = 35см.