Решите, пожалуйста, желательно добавьте во вложении, и объясните подробнее

Question

Решите, пожалуйста, желательно добавьте во вложении,
и объясните подробнее

---

Answer 1

1)
При x = 1 будет f(x) = √9 = 3 - это минимальное значение.
Максимальное значение никак не ограничено.
E(f) = [3; +oo)

2)

Но
E(f)=[3; 4]

3)
Минимум будет при sin x = -1, тогда cos x = 0; f(x) = -4-3*0 = -4
Максимум будет при sin x = 1, тогда cos x = 0; f(x) = 4 - 3*0 = 4
E(f) = [-4; 4]

4)
При x = 3 будет f(x) = 0 + 2 + 1/(0 + 1) = 2 + 1 = 3
Максимальное значение никак не ограничено.
E(f) = [3; +oo)

Comments

а для третьего примера есть другая запись, немного не понятно((?

---

Можно через производные, вы это проходили?

---

Вольфрам Альфа показывает, что ответ для 3) E(f) = [-5; 5]. Как это получить, я не знаю.

---

а если посмотреть производную... то tg(x) = -4/3 --- тангенс отрицателен во 2 четверти, т.е. ни cos(x)=0, ни sin(x)=1 или -1 к экстремуму никакого отношения не имеют...

---

Во-первых, я подозреваю, что они производную еще не проходили. А во-вторых, как из tg x = -4/3 получить f(x) = 5 ?

---

из tg x = -4/3 получилось, что максимум совсем НЕ при sin x = 1

---

Согласен, я ответил неправильно, но я все равно не понимаю, как решить эту задачу. А тем более, как ее решить БЕЗ производных.

---

во-первых, никто не запрещал применять производную --- задача не для 7 класса...

---

а ответ в любом случае должен быть правильным))

Answer 2

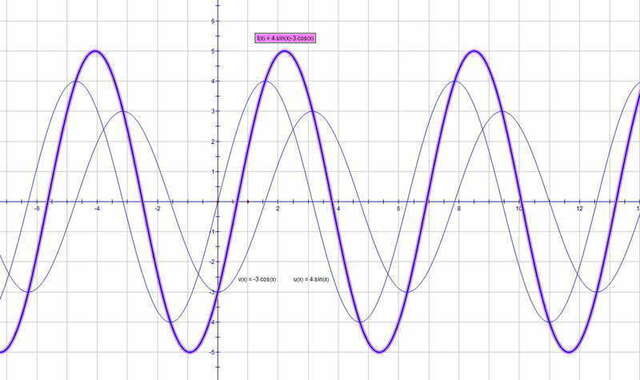
Про 3) можно посмотреть рис.
и станет понятно, что функция достигает максимума не тогда,
когда просто синус=1, а еще и значения косинуса нужно учитывать...
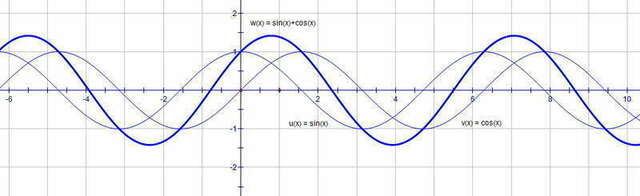
ведь максимум функции, например, sin(x)+cos(x) наступает отнюдь не для угла в 90 градусов, а как раз таки при х=45 градусов, когда складываются √2/2 + √2/2 ===и получается совсем не единица, а √2 (просто для иллюстрации рис.2)))
потому и Е(у) [-5; 5]

---

---