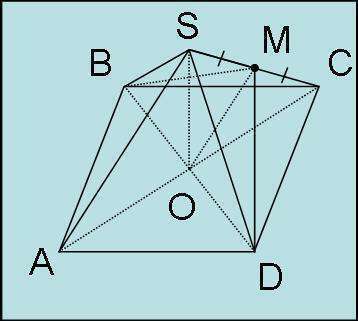
Надо доказать, что углы SMO и SMD прямые
Т.к. все ребра равны (путь a), то треугольник SCD - равносторонний значит DM является и медианой и высотой, т.е. угол DMS=90
Т.к. AB=AD=a то по т. Пифагора 
Так же по т.Пифагора: 
Т.к. CO=OD=SO то треугольник SOC равнобедренный, ОМ - медина и высота то угол SMO=90