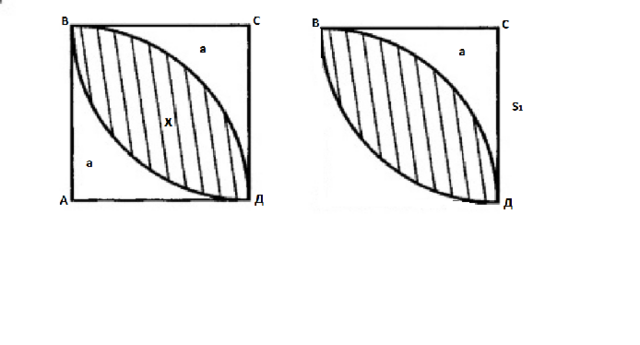
Заметим, что большая часть задач, где нужно найти площадь заштрихованной части, решается однотипно: из окружающей фигуры вычитают площадь незаштрихованной части, после чего остается площадь заштрихованной. Площадь заштрихованной части квадрата равна разности между его полной площадью и двух его угловых незаштрихованных частей при вершинах А и С
Эти части равны.
Пусть для удобства записи площадь квадрата будет S, площадь заштрихованной фигуры S(х), площадь незаштрихованного уголка квадрата при вершинах А и С - S(а)
Фигура ВСД ( на приложенном рисунке она дана отдельно ) - это четверть круга радиусом 8, т.к. сторона квадрата является радиусом этой окружности.
Площадь квадрата равна квадрату его стороны:
S= 8²=64 см²
Обозначим площадь четверти круга S1
S1=πr² :4
S(1)=64π:4=16π см²
Тогда незаштрихованная часть квадрата при вершине А имеет площадь
S(а)=S АВСД- S(1)⇒
S(а) = 64-16π см²
Площадь заштрихованной на рисунке части будет равна площади четверти круга без S(а).
S(х)=S(1)-S(a)
S(х)=16π-(64-16π)=32π-64 см²
S(х)=16π-(64-16π)=32(π-2)
Примем π=3,14
S(х)=32*1,14=36,48 см²