Найдите боковую поверхность правильной треугольной пирамиды,если сторона основания равна...

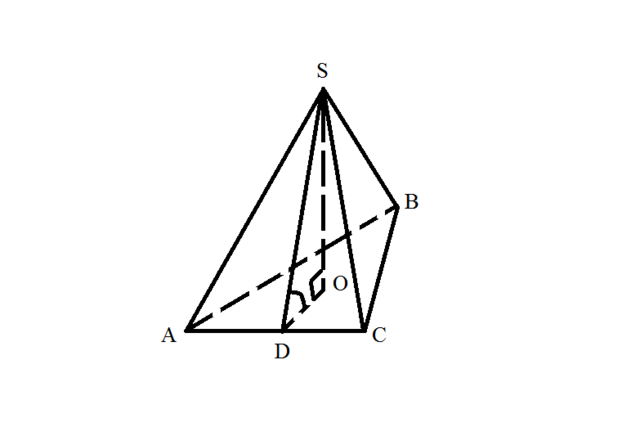
Проведем апофему SD и высоту SO (см. приложение). Так как в треугольнике SOD угол SDO = 30°, то катет SO = 0,5SD. Пусть, SO = x см, тогда SD = 2x. Зная, что OD - это радиус вписанной в правильный треугольник окружности, который равен $\frac{a}{2 \sqrt{3} }$ , где а - сторона треугольника, составим уравнение пользуясь теоремой Пифагора:
$x^{2} + \frac{1}{3}=4 x^{2} \\ 3 x^{2} = \frac{1}{3} \\ x^{2} = \frac{1}{9} \\ x= \frac{1}{3}$
Значит, апофема SD = $\frac{2}{3}$ . Значит, площадь треугольника SAC = $\frac{1}{2} *2* \frac{2}{3} =\frac{2}{3}$ . А площадь боковой поверхности равна: $3*\frac{2}{3}= 2$ см²
Ответ: 2 см²