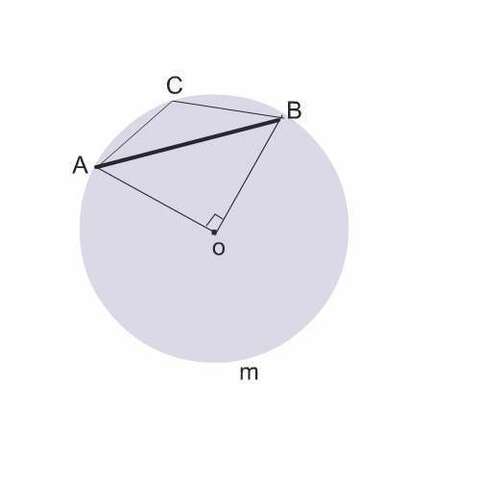
Соединим центр О окружности с концами А и В данной хорды.
Поскольку хорда равна 30√2, а радиус окружности 30, получим равнобедренный
треугольник с равными углами при основании АВ.
sin ВАО=sin АВО=30:30√2=1/√2=√2/2Это синус 45°
Так как углы при основании АВ равны 45°, угол АОВ=90°
Тогда центральный угол АОВ, опирающийся на бóльшую дугу АmВ, равен
360°-90°=270°
Вписанный тупой угол АСВ, опирающийся на ту же дугу, равен половине центрального угла и равен
270°:2=135°.