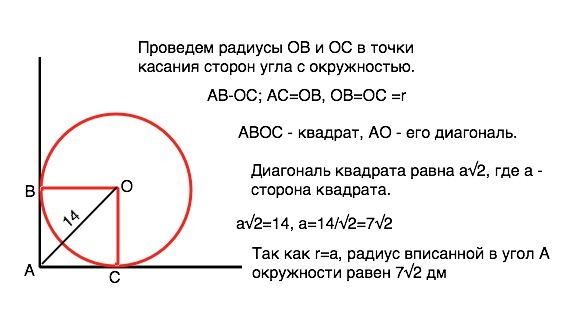
Проведем радиусы ОВ и ОС в точки касания сторон угла с сокружностью. Радиус, проведенный к касательной в точку касания, перпендикулярен касательной.
АВ-ОС; АС=ОВ; ОВ=ОС =r
АВОС - квадрат, АО - его диагональ.
Диагональ квадрата равна а√2, где а - сторона квадрата.
а√2=14, а=14/√2=7√2
Так как r=a, радиус вписанной в угол А окружности равен 7√2 дм