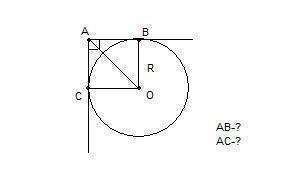
2. Используем свойство касательных к окружности, проведенных из одной точки: отрезки касательных к окружности (это АВ и АС в нашем случае), проведенные из одной точки (точка А), равны и составляют равные углы с прямой, проходящей через эту точку и центр окружности. Т.е. АВ=АС, Рассмотрим четырехугольник АВОС. Все углы его прямые (угол А прямой по условию, углы ОВА и ОСА прямые, т.к. касательные АВ и АС к окружности перпендикулярны к радиусу, проведенному в точки касания В и С. Оставшийся неизвестным Рассмотрим прямоугольный треугольник АВО. Зная, что сумма острых углов прямоугольного треугольника равна 90°, находим угол ВОА:BOA=90-Таким образом, прямоугольный треугольник АВО - равнобедренный (углы при его основании АО равны).
АВ=ОВ=R. Выше показано, что АВ=АС, значит АВ=АС=R.