В треугольнике ABC проведена медиана BM, ** стороне AB взята точка K так, что AK=1/3AB....

Question

В треугольнике ABC проведена медиана BM, на стороне AB взята точка K так, что AK=1/3AB. Площадь треугольника AMK равна 5. Найдите площадь треугольника ABC.

Answer 1

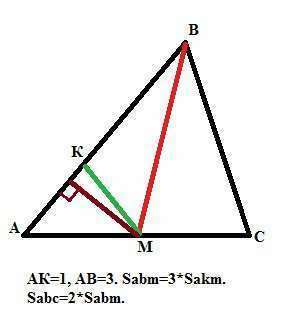
Так как  AK:AB=1:3, то Sakm:Sabm=1:3, так как отношение площадей треугольников с одинаковой высотой, опущенной на соответствующие стороны, равно отношению этих сторон. Значит площадь треугольника АВМ в три раза больше площади треугольника АКМ. Sabm=15.  Sabm= (1/2)*Sabc (так как ВМ - медиана, а медиана делит треугольник на два равновеликих треугольника). Отсюда Sabc=30.
Ответ: Sabc=30 квадратных единиц.

---