** рисунке изображён график функции, к которому проведены касательные в четырёх точках....

Question

На рисунке изображён график функции, к которому проведены касательные
в четырёх точках.
Ниже указаны значения производной в данных точках. Пользуясь графиком,
поставьте в соответствие каждой точке значение производной в ней.
ТОЧКИ:
А )K
Б) L
В) M
Г) N
ЗНАЧЕНИЯ ПРОИЗВОДНОЙ:
1)−4
2) 3
3) 2/3
4) −0,5

---

Answer 1

Геометрический смысл производной в точке
f`(x₀)= k (касательной)
k(касательной)=tgα, α - угол наклона касательной (прямой) к оси ох.

Так как функция тангенс возрастает на (-π/2; π/2), то большему значению  аргумента соответствует большее значение тангенса.

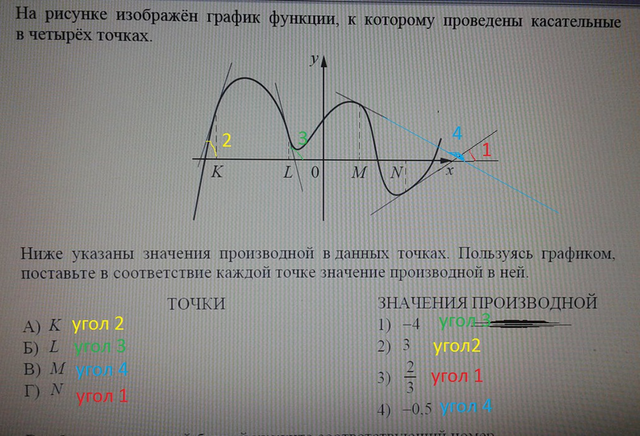
угол 1 и угол 2 образуют острые углы с осью ох. Тангенс острого угла положителен.
Угол 2 больше угла 1, значит углу 2 соответствует значение производной равное 3, а углу 1 соответствует значение производной, равное 2/3.

Углы 3 и 4 тупые. А смежные к ним острые.
Смежный углу 3 больше, чем смежный к углу 4. Значит, тангенс  смежного с углом 3  равен |-4|=4, угол 3 имеет тангенс, равный (-4) и значение производной соответственно (-4).
См. рисунок в приложении.

---