При каких значениях a прямая y=a-x имеет 1 решение с системой:

Question

Дан 1 ответ

Правильный ответ

$\begin{cases}y^2-xy-4y+2x+4=0\\ x+4 \geq 0\\ 5-y\ \textgreater \ 0\end{cases}$

Перед нами система уравнения неравенств. Решать эту задачу будем графическим методом. Для этого нужно все выразить через y и построить графики.
Преобразуем систему:

$\begin{cases}y^2-xy-4y+2x+4=0\\ x+4 \geq 0\\ 5-y\ \textgreater \ 0\end{cases}=\ \textgreater \ \begin{cases}y^2-y(x+4)+2x+4=0\\ x \geq -4\\ y\ \textless \ 5\end{cases}$

Поработаем с первым уравнением системы:

$y^2-y(x+4)+2x+4=0$

Это квадратное уравнение, которое можно решать относительно y.

$D=(x+4)^2-4(2x+4)=x^2+8x+16-8x-16=x^2\\\\y_1=\frac{x+4+x}2=\frac{2x+4}2=\frac{2(x+2)}2=x+2\\\\y_2=\frac{x+4-x}2=\frac{4}2=2$

Мы получили 2 прямых, множество точек которых и есть решение данного уравнения.

Теперь исходная система выглядит таким образом:

$\begin{cases} \left[\begin{array}{ccc}y=x+2\\y=2\end{array}\right\\ x\geq -4\\ y \ \textless \ 5\end{cases}$

$x \geq -4$ и $y\ \textless \ 5$ это что-то типа "ограничителей" за эти пределы наши прямые не смогут выходить.

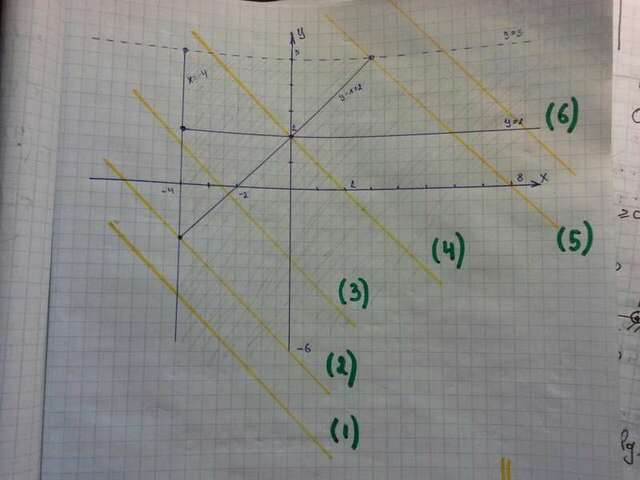
Построим графики вместе с ограничителями. (см. рисунок)

Карандашом отмечена область в которой существуют графики (эта область после ограничения).
Ограничитель $y\ \textless \ 5$ отмечен штрихованной линией, так как неравенство строгое.
Ограничитель $x \geq -4$ прорисован, так как неравенство не строгое.
После того как все построили мы должны разобраться в каких случаях прямая   $y=-x+a$ имеет с системой всего 1 корень.
Достаточно, чтобы эта прямая имела 1 точку пересечения с любой из прямых: $y=x+2,y=2$

$y=-x+a$ - множество прямых $y=-x$ которые "двигаются" по оси $y$ вверх и вниз.
Мы должны двигать прямую   $y=-x+a$ снизу вверх и смотреть, в каких случаях она имеет всего 1 точку пересечения с этими прямыми.

Желтыми линиями обозначены все возможные варианты положения прямой $y=-x+a$ зеленые цифры - нумерация положения этой прямой.

(1): Прямая $y=-x+a$ не имеет общий точек пересечения с прямыми $y=x+2$ и $y=2$
(2): В этом положении прямая    $y=-x+a$ все еще имеет 1 общую точку пересечения c прямой $y=x+2$ ,если мы сдвинем прямую $y=-x+a$ чуть выше то она будет иметь так-же 1 общую точку пересечения. Это демонстрирует (3) положение прямой    $y=-x+a$
Мы получаем часть ответа: $a\in[-6;-2]$
(4): В этой точке прямая    $y=-x+a$ имеет всего 1 общую точку пересечения. Еще часть ответа: $a=2$
Далее прямая    $y=-x+a$ имеет 2 точки пересечения, пока не доходит до (5) положения. В этом положении прямая    $y=-x+a$ пересекается только с прямой $y=2$
И дальше до бесконечности будет пересекаться только с этой прямой, это демонстрирует (6) положение.
Еще часть ответа: $a\in[8;+\infty)$

Ответ: $a\in[-6;-2]U[2]U[8;+\infty)$

аноним 04 Апр, 18