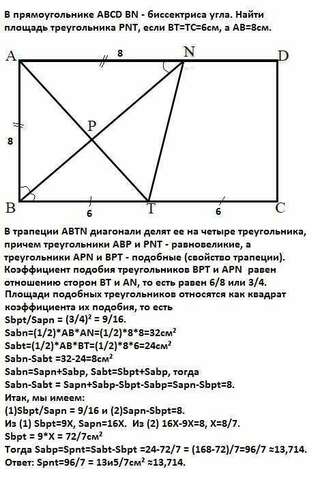
В прямоугольнике АВСD, изображенном на рисунке, BN - биссектриса.
Найдите площадь треугольника РNТ, если ВТ=ТС=6см, а АВ=8см.
___________________________________________________________
В трапеции АВТN диагонали делят ее на четыре треугольника, причем треугольники АВР и РNТ - равновеликие, а треугольники АРN и ВРТ - подобные (свойство трапеции).
Коэффициент подобия треугольников ВРТ и АРN равен отношению сторон ВТ и АN, то есть равен 6/8 или 3/4.
Площади подобных треугольников относятся как квадрат коэффициента их подобия, то есть Sbpt/Sapn = (6/8)²=(3/4)² = 9/16.
Sabn=(1/2)*AB*AN=(1/2)*8*8=32cм²
Sabt=(1/2)*AB*BT=(1/2)*8*6=24cм²
Sabn-Sabt =32-24=8см²
Sabn=Sapn+Sabp, Sabt=Sbpt+Sabp, тогда
Sabn-Sabt = Sapn+Sabp-Sbpt-Sabp=Sapn-Sbpt=8см².
Итак, мы имеем:
(1)Sbpt/Sapn = 9/16 и (2)Sapn-Sbpt=8см².
Из (1) Sbpt=9Х, Sapn=16Х. Из (2) 16Х-9Х=8, Х=8/7.
Sbpt = 9*Х = 72/7см²
Тогда Sabp=Sрnt=Sabt-Sbpt =24-72/7 = (168-72)/7=96/7 ≈13,714.
Ответ: Sрnt=96/7 = 13и5/7см² ≈13,71