Две окружности касаются внутренним образом в точке M. Пусть AB — хорда большей...

Question

Две окружности касаются внутренним образом в точке M. Пусть AB — хорда большей окружности, касающаяся меньшей окружности в точке T. Известно, что AT=7, BT=4. Найдите отношение AM/BM

Answer 1

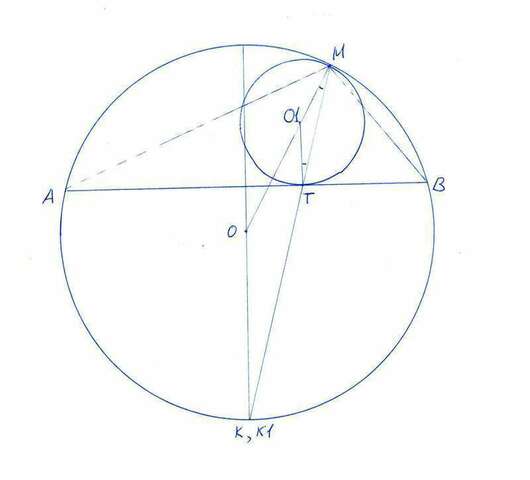
Пусть KO - диаметр большей окружности, перпендикулярный AB. Точка K лежит на большей окружности.
Ясно, что KO II O1T; так как O1T тоже перпендикулярно AB.
Пусть прямая MT пересекает прямую KO в точке K1.
На чертеже эти точки K и K1 изображены, как одна - но именно это и есть предмет доказательства. Я буду доказывать, что точки K и K1 совпадают.
На самом деле все уже очевидно - треугольники OK1M и O1TM подобны, а треугольник O1TM очевидно равнобедренный :). Поэтому OK1 = OM = OK, и точки K и K1 совпадают.
Это означает, что прямая MT, будучи продолжена за точку T, делит дугу AKB пополам (я напомню, что KO - диаметр, перпендикулярный хорде AB, поэтому точка K делит дугу AKB пополам. ).
Углы AMK и BMK - вписанные и опираются на равные дуги, поэтому они равны. Следовательно MT - биссектриса угла AMB;
AM/MB = AT/BT = 7/4;

---

Comments

огромное спасибо

---

неверно

---

Да неужто? :)))))

---

КО не диаметр, а радиус. Вы делаете предположения из рисунка "очевидно - треугольники OK1M и O1TM подобны, а треугольник O1TM очевидно равнобедренный", но нет доказательств.

---

Ого! кто-то высказался :))))))))) если это - не болтовня, могу ответить. Прямая задается ДВУМЯ точками, через которые проходит. Прямая KO - диаметр, в том смысле, что проходит через центр большой окружности (и не более того). Ну пусть она "радиус". :))) многое сразу изменилось :))) Второе. "Очевидно - треугольники OK1M и O1TM подобны" потому что OK II O1T (ах да, специально для вас - OK1 II O1T :))) ) - именно поэтому очевидно. Ну, может, ВАМ не очевидно. Про равнобедренность надо? :))

---

Нет доказательств :) если вам нужны доказательства, что два треугольника с равными углами подобны, то мои решения вам читать не надо. Я всегда пишу решения так, что над ними надо думать. И никогда не "помогаю" тем, кто думать не хочет.

---

Кстати, в этом решении еще много такого, что "не доказано" :) к примеру, почему диаметр (ДИАМЕТР), перпендикулярный хорде, дели её пополам (или - почему диаметр-радиус, делящий хорду пополам, ей перпендикулярен). Далее, не доказано, почему точка K делит пополам дугу A(K)B. В самом деле, почему? :)))