Диагональ боковой грани правильной треугольной призмы наклонена к плоскости основания под...

Question

Диагональ боковой грани правильной треугольной призмы наклонена к плоскости основания под углом альфа, а площадь этой грани равна Q. Найдите площадь полной поверхности

Comments

Мало баллов.

---

Сочувствую

Answer 1

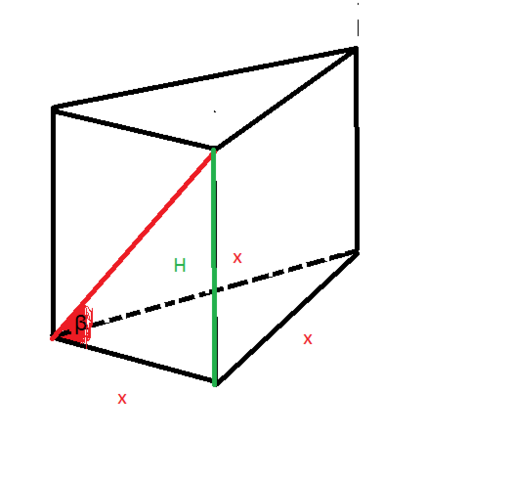
Пусть сторона основания равна х
Из прямоугольного треугольника с острым углом β найдем
Н=х·tgα
Тогда площадь боковой грани равна произведению стороны х на высоту Н
Q=x·xtgα  ⇒  x=√(Q/tgα)
S ( полн)=S (бок) + 2 S(осн)=3х·Н+2·х²√3/4=3·√(Q/tgα)·√(Q/tgα)·tgα+(Q/tgα)·(√3/2)=
(Q/tgα)·(3tgα+(√3/2))
Ответ. S=(Q/tgα)·(3tgα+(√3/2))

---

Comments

Спасибо!Хорошо что не мне это ))))

---

Да, эта задача намного труднее. Метод введения переменной. Выразить известное данное Q через эту переменную.

---

пусть сам разбирается)

---

Это и вам полезно. Так что разбирайтесь вместе

---

)))