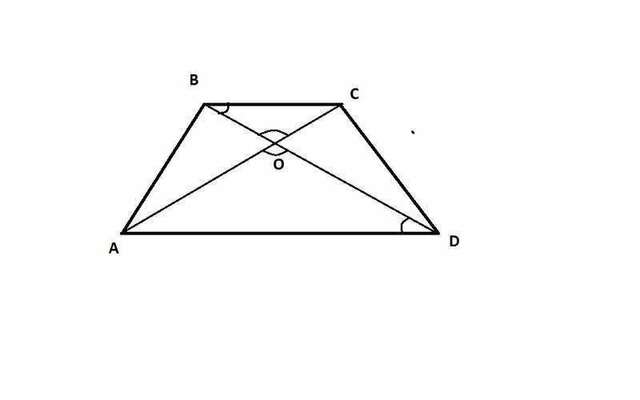
Если О расположена на пересечении диагоналей трапеции, а АD и BC - основания трапеции, то:
1) Углы О в треугольниках BOC и DOA равна как вертикальные;
2) Так как в трапеции основания - параллельные прямые, то диагональ ВD - cекущая при параллельных прямых. Значит углы СBO и ADO равны как внутренние накрест лежащие углы.
Если два угла одного треугольника равны двум углам другого треугольника, то такие треугольники подобны. Что и требовалось доказать/