Через точку O пересечения диагоналей параллелограмма ABCD проведен отрезок EF||AB, где...

Question

Через точку O пересечения диагоналей параллелограмма ABCD проведен отрезок EF||AB, где точки E и F принадлежат соответственно сторонам BC и AD
параллелограмма. Сумма диагоналей равна 28 см. Разность между периметрами треугольников AOF и BOE равна 9 см. Найдите диагонали параллелограмма

Answer 1

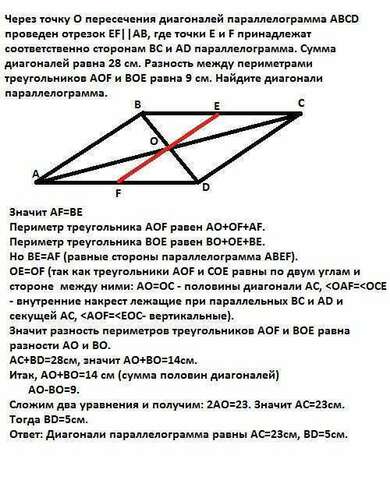
АВЕF - параллелограмм, так как ВЕ||АF, а АВ||ЕF.
Значит АF=BE
Периметр треугольника АОF равен АО+ОF+АF.
Периметр треугольника ВОЕ равен ВО+ОЕ+ВЕ.
Но ВЕ=АF (равные стороны параллелограмма АВЕF).
ОЕ=ОF (так как треугольники АОF и СОЕ равны по двум углам и стороне 
между ними: АО=ОС - половины диагонали АС, накрест лежащие при параллельных ВС и АD и секущей АС,
Значит разность периметров треугольников АОF и ВОЕ равна разности
АО и ВО.
АС+ВD=28см, значит АО+ВО=14см.
Итак, АО+ВО=14 см (сумма половин диагоналей)
         АО-ВО=9.
Сложим два уравнения и получим: 2АО=23. Значит АС=23см.
Тогда ВD=5см.
Ответ: Диагонали параллелограмма равны АС=23см, ВD=5см.

---