В равнобедренной трапеции АВСD боковые стороны и меньшее основание равны. Острый угол А равен α.
Найти радиус окружности, описанной около треугольника АВС.
--
Трапеция равнобедренная, следовательно, вокруг нее можно описать окружность, и это будет одна и та же описанная окружность и для треугольника АВС.
Треугольник АВС - равнобедренный.
Угол ВАС=углу ВСА.
Но угол ВСА - накрестлежащий с углом САD и равен ему.
Следовательно, углы ВАС и САD равны, ⇒ АС - биссектриса и делит угол А на два величиной по α/2
Опустим перпендикуляр из вершины В и продолжим до пересечения с окружностью в точке Е.
Соединим Е и С. Угол СВЕ - прямой, следовательно, ЕС - диаметр описанной окружности.
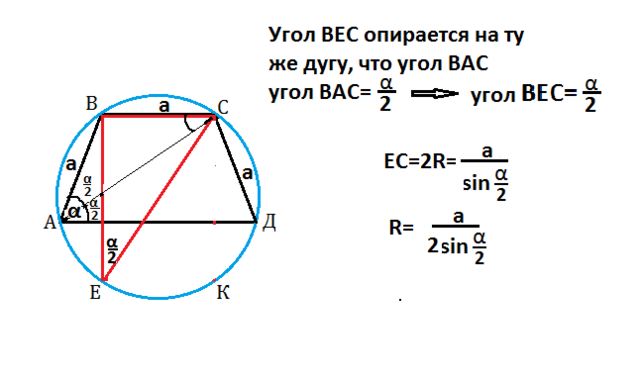
Вписанный угол ВЕС= вписанному углу ВАС, так как опирается на ту же дугу.
Угол ВЕС=α/2
ЕС=2R
EC=a:sin0,5α
R=(a:sin0,5α):2