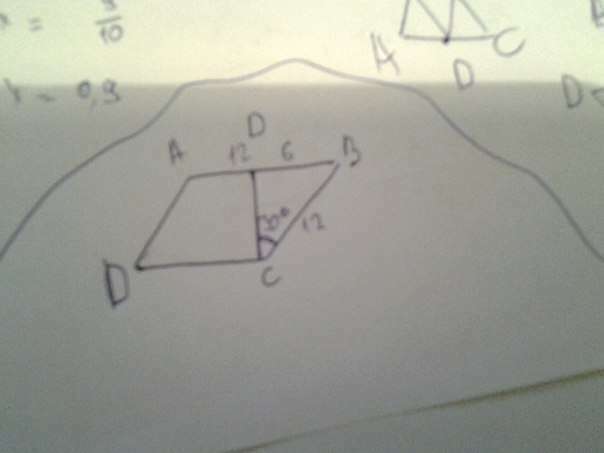
Вообщем. Из всех данных рассмотрим треугольник CDB. Он прямоугольный, его сторона DB=AD, так как CD делит AB пополам, от сюда следует, что DB равно 6 см. Теперь найдём гипотенузу этого треугольника. Угол DCB равен 30 градусам, так написано в дано. Вспоминаем волшебную теоремку, что катет лежащий на против угла в 30 градусов равен половине гипотенузы. У нас катет на против этого угла равен 6 см, значит гипотенуза равна 12 см, а от сюда мы можем посчитать периметр, так, как противолежащие стороны параллелограмма равны, получается 12+12+12+12=48.
Ответ: Р=48 см.