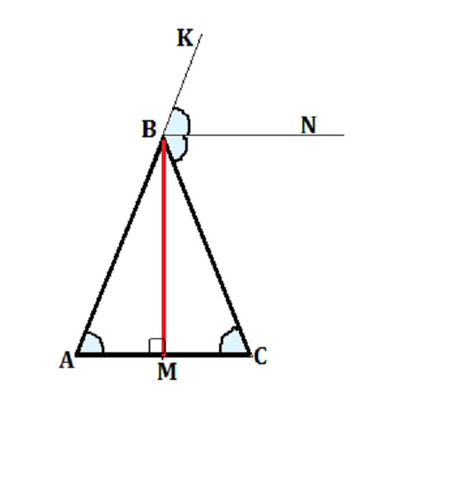
Дан треугольник АВС.
ВN || AC
Угол КВС- внешний при вершине В.
∠ KBN= ∠NBC по условию (BN - биссектриса)
∠ KBN=∠ BAC как соответственные при параллельных прямых BN и АС и секущей КА
∠NBC=∠ВCA как накрестлежащие.
⇒
∠ВАМ=
∠ВСМ
и Δ АВС - равнобедренный. ⇒
ВМ - медиана и высота равнобедренного треугольника АВС.
⇒
∠ВМС=90º
Т.к. BN || АС, угол МВN= углу ВМС=90º