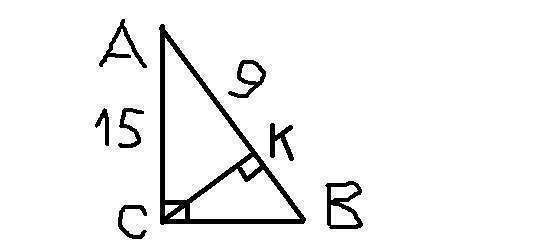Проведем высоту из угла С прямоугольного треугольника ABC на гипотенузу AC. Из условия задачи ясно, что AC=15 см, CK=9 см. Заметим, что треугольники ABC и ACK подобны по двум углам. У треугольника ABC - угол С прямой, у треугольника ACK - угол К прямой. Угол А у этих треугольников общий. Выполняется признак подобия по 3-м углам. Узнаем коэффициент подобия этих треугольников. К углу А прилежащим катетом в треугольнике АВС будет сторона АС, а в треугольнике АСК, прилежащей к углу А будет сторона АК. Значит коэффициентом подобия этих треугольников будет отношение сторон АС и АК.

Вычислить площадь треугольника АКС - нетрудно. Надо узнать сторону СК по теореме Пифагора




CК=12 см.
Площадь треугольника АКС равна половине произведения АК на АС.



 .
.
Так как треугольники подобны, то площадь треугольника АВС равна произведению квадрата подобия этих треугольников на площадь треугольника АКС



Ответ: